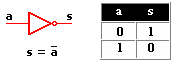
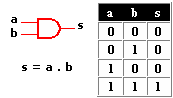
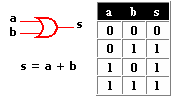
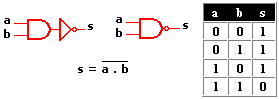
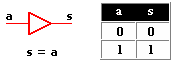
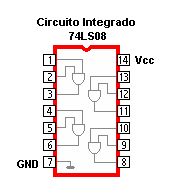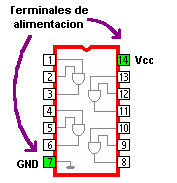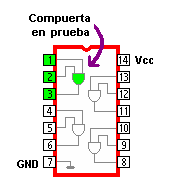
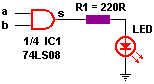
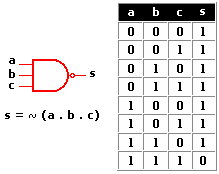
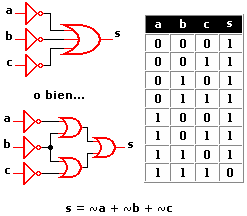
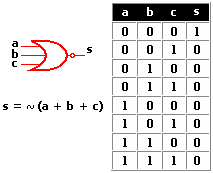
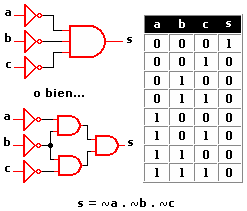
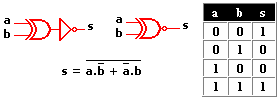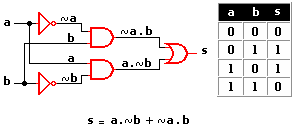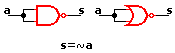Circuitos integrados digitales . Los circuitos integrados son la base fundamental del desarrollo de la electrónica en la actualidad, debido a la tendencia a facilitar y economizar las tareas del hombre. Los circuitos cuyos componentes realizan operaciones análogas a las que indican los operadores lógicos se llaman "Circuitos Lógicos" o "circuitos digitales". Los Circuitos Lógicos están compuestos por elementos digitales como la compuerta AND (Y), compuerta OR (O), compuerta NOT (NO) y otras combinaciones muy complejas de los circuitos antes mencionados.
Tipos de Elementos Digitales
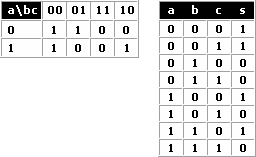
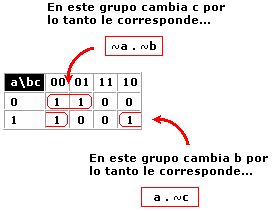
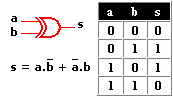
Estas combinaciones (ya mencionadas) dan lugar a otros tipos de elementos digitales. Aquí hay un listado de estos. · Compuerta NAND (No Y) · Compuerta NOR (No O) · Compuerta OR exclusiva (O exclusiva) · Mutiplexores o multiplexadores · Demultiplexores o demultiplexadores · Decodificadores · Codificadores · Memorias · flip-flops · Micro Procesadores · Micro Controladores
Familias Lógicas
Los circuitos digitales emplean componentes encapsulados, los cuales pueden albergar puertas lógicas o circuitos lógicos más complejos. Estos componentes están estandarizados, para que haya una compatibilidad entre fabricantes, de forma que las características más importantes sean comunes. De forma global los componentes lógicos se engloban dentro de una de las dos familias siguientes: TTL: diseñada para una alta velocidad. CMOS: diseñada para un bajo consumo. Actualmente dentro de estas dos familias se han creado otras, que intentan conseguir lo mejor de ambas: un bajo consumo y una alta velocidad. La familia lógica ECL se encuentra a caballo entre la TTL y la CMOS. Esta familia nació como un intento de conseguir la rapidez de TTL y el bajo consumo de CMOS, pero en raras ocasiones se emplea.
Dentro de la familia TTL encontramos las siguiente sub-familias :
L: Low power = dsipación de potencia muy baja
LS: Low power Schottky = disipación y tiempo de propagación pequeño.
S: Schottky = disipación normal y tiempo de propagación pequeño.
AS: Advanced Schottky = disipación normal y tiempo de propagación extremadamente pequeño. Tension De Alimentacion
CMOS: 5 a 15 V (dependiendo de la tensión tendremos un tiempo de propagación). TTL : 5 V.Parámetros de puerta
Las puertas lógicas no son dispositivos ideales, por lo que vamos a tener una serie de limitaciones impuestas por el propio diseño interno de los dispositivos lógicos. Internamente la familia TTL emplea transistores bipolares (de aquí su alto consumo), mientras que la familia CMOS emplea transistores MOS (a lo que debe su bajo consumo).
Información General
La electrónica moderna usa electrónica digital para realizar perfeccionamientos en la tecnología, muchas veces nos vemos frente a éstos sin darnos cuenta, el llamado efecto "Caja Negra". En el circuito lógico digital existe transmisión de información binaria entre sus circuitos. A primera instancia esto nos parece relativamente simple, pero los circuitos electrónicos son bastante complejos ya que su estructura esta compuesta por un número muy grande de circuitos simples, donde todos deben funcionar de la manera correcta, para lograr el resultado esperado y no obtener una información errónea. La información binaria que transmiten los circuitos ya mencionados, se representan de la siguiente forma: · "0" o "1" · "Falso" o "Verdadero" · "On" y "Off" · "Abierto" o "Cerrado" · o cualquier mecanismo que represente dos estados mutuamente excluyentes
Circuito | |
|---|---|
 |
Circuito Impreso. En Electrónica, un circuito impreso o PCB (del inglés Printed Circuit Board), es un medio para sostener mecánicamente y conectar eléctricamente componentes electrónicos, a través de rutas o pistas de material conductor, grabados en hojas de cobre laminadas sobre un sustrato no conductor.
Los circuitos impresos son robustos, baratos, y habitualmente de una fiabilidad elevada aunque de vez en cuando pueda tener fallos técnicos. Requieren de un esfuerzo mayor para el posicionamiento de los componentes, y tienen un coste inicial más alto que otras alternativas de montaje, como el montaje punto a punto (o wire-wrap), pero son mucho más baratos, rápidos y consistentes en producción en volúmenes.
Historia
El inventor del circuito impreso es probablemente el ingeniero austriaco Paul Eisler (1907-1995) quien, mientras trabajaba en Inglaterra, hizo uno alrededor de 1936, como parte de una radio. Alrededor de 1943, los Estados Unidos comenzaron a usar esta tecnología en gran escala para fabricar radios que fuesen robustas, para la Segunda Guerra Mundial. Después de la guerra, en 1948, EE.UU. liberó la invención para el uso comercial. Los circuitos impresos no se volvieron populares en la electrónica de consumo hasta mediados de 1950, cuando el proceso de Auto-Ensamblajefue desarrollado por la Armada de los Estados Unidos
Antes que los circuitos impresos (y por un tiempo después de su invención), la conexión punto a punto era la más usada. Para prototipos, o producción de pequeñas cantidades, el método 'wire wrap' puede ser más eficiente..
Originalmente, cada componente electrónico tenía patas de alambre, y el circuito impreso tenía orificios taladrados para cada pata del componente. Las patas de los componentes atravesaban los orificios y eran soldadas a las pistas del circuito impreso. Este método de ensamblaje es llamado through-hole ( "a través del orificio", por su nombre en inglés). En 1949, Moe Abramson y Stanilus F. Danko, de la United States Army Signal Corps desarrollaron el proceso de Autoensamblaje, en donde las patas de los componentes eran insertadas en una lámina de cobre con el patrón de interconexión, y luego eran soldadas. Con el desarrollo de la laminación de tarjetas y técnicas de grabados, este concepto evolucionó en el proceso estándar de fabricación de circuitos impresos usado en la actualidad. La soldadura se puede hacer automáticamente pasando la tarjeta sobre un flujo de soldadura derretida, en una máquina de soldadura por ola.
Sin embargo, las patas y orificios son un desperdicio. Es costoso perforar los orificios, y el largo adicional de las patas es eliminado. En vez de utilizar partes through-hole, a menudo se utilizan dispositivo de montaje superficial.
Tipos de circuitos impresos
Multicapa: Es lo más habitual en productos comerciales. Suele tener entre 8 y 10 capas, de las cuales algunas están enterradas en el sustrato.
2-sided plated holes: Es un diseño complicado de bajo coste con taladros metalizados que nos permite hacer pasos de cara.
Single-sided non-plated holes: Es un PCB con agujeros sin metalizar. Se usa en diseños de bajo coste y sencillos.
2-sided non-plated holes: Diseño sencillo con taladros sin metalizar. Sustrato de fibras de vidrio y resina. Hay que soldar por los dos lados para que haya continuidad.
Composición física
La mayoría de los circuitos impresos están compuestos por entre una a dieciséis capas conductoras, separadas y soportadas por capas de material aislante (sustrato) laminadas (pegadas) entre sí.
Las capas pueden conectarse a través de orificios, llamados vías. Los orificios pueden ser electorecubiertos, o se pueden utilizar pequeños remaches. Los circuitos impresos de alta densidad pueden tener vías ciegas, que son visibles en sólo un lado de la tarjeta, o vías enterradas, que no son visibles en el exterior de la tarjeta.
Sustratos
Los sustratos de los circuitos impresos utilizados en la electrónica de consumo de bajo costo, se hacen de papel impregnados de resina fenólica, a menudo llamados por su nombre comercial Pértinax. Usan designaciones como XXXP, XXXPC y FR-2. El material es de bajo costo, fácil de mecanizar y causa menos desgaste de las herramientas que los sustratos de fibra de vidrio reforzados. Las letras "FR" en la designación del material indican "retardante de llama" (Flame Retardant en inglés).
Los sustratos para los circuitos impresos utilizados en la electrónica industrial y de consumo de alto costo, están hechos típicamente de un material designado FR-4. Éstos consisten de un material de fibra de vidrio, impregnados con una resina epóxica resistente a las llamas. Pueden ser mecanizados, pero debido al contenido de vidrio abrasivo, requiere de herramientas hechas de carburo de tungsteno en la producción de altos volúmenes. Debido al reforzamiento de la fibra de vidrio, exhibe una resistencia a la flexión y a las trizaduras, alrededor de 5 veces más alta que el Pertinax, aunque a un costo más alto.
Los sustratos para los circuitos impresos de circuitos de radio frequencia de alta potencia usan plásticos con una constante dieléctrica (Permitividad) baja, tales como Rogers® 4000, Rogers® Duroid, (DuPont Teflón) (tipos GT y GX), Poliamida, Polies (Poliamida, Poliestireno) y poliestireno entrecruzado. Típicamente tienen propiedades mecánicas más pobres, pero se considera que es un compromiso de ingeniería aceptable, en vista de su desempeño eléctrico superior.
Los circuitos impresos utilizados en el vacío o en gravedad cero, como en una nave espacial, al ser incapaces de contar con el enfriamiento por convección, a menudo tienen un núcleo grueso de cobre o aluminio para disipar el calor de los componentes electrónicos.
No todas las tarjetas usan materiales rígidos. Algunas son diseñadas para ser muy o ligeramente flexibles, usando DuPonts Kapton film de poliamida y otros. Esta clase de tarjetas, a veces llamadas circuitos flexibles, o circuitos rígido-flexibles, respectivamente, son difíciles de crear, pero tienen muchas aplicaciones. A veces son flexibles para ahorrar espacio (los circuitos impresos dentro de las cámaras y audífonos son casi siempre circuitos flexibles, de tal forma que puedan doblarse en el espacio disponible limitado. En ocasiones, la parte flexible del circuito impreso se utiliza como cable o conexión móvil hacia otra tarjeta o dispositivo. Un ejemplo de esta última aplicación es el cable que conecta el cabezal en una impresora de inyección de tinta.
Características básicas del sustrato
Mecánicas
- Suficientemente rígidos para mantener los componentes.
- Fácil de taladrar.
- Sin problemas de laminado.
Químicas
- Metalizado de los taladros.
- Retardante de las llamas.
- No absorbe demasiada humedad.
Térmicas
- Disipa bien el calor.
- Coeficiente de expansión térmica bajo para que no se rompa.
- Capaz de soportar el calor en la soldadura.
- Capaz de soportar diferentes ciclos de temperatura.
Eléctricas
- Constante dieléctrica baja para tener pocas pérdidas a altas.
- Punto de ruptura dieléctrica alto.
Diseño
Usualmente un ingeniero eléctrico o electrónico diseña el circuito y un especialista diseña el circuito impreso. El diseñador debe obedecer numerosas normas para diseñar un circuito impreso que funcione correctamente y que al mismo tiempo sea barato de fabricar.
Diseño electrónico automatizado
Los diseñadores de circuitos impresos a menudo utilizan programas de Diseño electrónico automatizado (EDA por sus siglas en inglés), para distribuir e interconectar los componentes. Estos programas almacenan información relacionada con el diseño, facilita la edición, y puede también automatizar tareas repetitivas.
La primera etapa es convertir el esquemático en una lista de nodos (o net list en inglés). La lista de nodos es una lista de las patas y nodos del circuito, a los que se conectan las patas de los componentes. Usualmente el programa de captura de esquemáticos, utilizado por el diseñador del circuito, es responsable de la generación de la lista de nodos, y esta lista es posteriormente importada en el programa de ruteo.
El siguiente paso es determinar la posición de cada componente. La forma sencilla de hacer esto es especificar una rejilla de filas y columnas, donde los dispositivos deberían ir. Luego, el programa asigna la pata 1 de cada dispositivo en la lista de componentes, a una posición en la rejilla. Típicamente, el operador puede asistir a la rutina de posicionamiento automático al especificar ciertas zonas de la tarjeta, donde determinados grupos de componentes deben ir. Por ejemplo, las partes asociadas con el subcircuito de la Fuente de alimentación se le podría asignar una zona cercana a la entrada al conector de alimentación. En otros casos, los componentes pueden ser posicionados manualmente, ya sea para optimizar el desempeño del circuito, o para poner componentes tales como perillas, interruptores y conectores, según lo requiere el diseño mecánico del sistema.
El computador luego expande la lista de componentes en una lista completa de las patas para la tarjeta, utilizando plantillas de una biblioteca de footprints asociados a cada tipo de componentes. Cada footprint es un mapa de las patas de un dispositivo, usualmente con la distribución de los pad y perforaciones recomendadas. La biblioteca permite que los footprint sean dibujados sólo una vez, y luego compartidos por todos los dispositivos de ese tipo.
En algunos sistemas, los pads de alta corriente son identificados en la biblioteca de dispositivos, y los nodos asociados son etiquetados para llamar la atención del diseñador del circuito impreso. Las corrientes elevadas requieren de pistas más anchas, y el diseñador usualmente determina este ancho.
Luego el programa combina la lista de nodos (ordenada por el nombre de las patas) con la lista de patas (ordenada por el nombre de las patas), transfiriendo las coordenas físicas de la lista de patas a la lista de nodos. La lista de nodos es luego reordenada, por el nombre del nodo.
Algunos sistemas pueden optimizar el diseño al intercambiar la posición de las partes y compuertas lógicas para reducir el largo de las pistas de cobre. Algunos sistemas también detectan automáticamente las patas de alimentación de los dispositivos, y generan pistas o vías al plano de alimentación o conductor más cercano.
Luego el programa trata de rutear cada nodo en la lista de señales-patas, encontrando secuencias de conexión en las capas disponibles. A menudo algunas capas son asignadas a la alimentación y a la tierra, y se conocen como plano de alimentación y tierra respectivamente. Estos planos ayudan a blindar los circuitos del ruido.
El problema de ruteo es equivalente al Problema del vendedor viajero, y es por lo tanto NP-completo, y no se presta para una solución perfecta. Un algoritmo práctico de ruteo es elegir la pata más lejana del centro de la tarjeta, y luego usar un algoritmo codicioso para seleccionar la siguiente pata más cercana con la señal del mismo nombre.
Después del ruteo automático, usualmente hay una lista de nodos que deben ser ruteados manualmente.
Una vez ruteado, el sistema puede tener un conjunto de estrategias para reducir el costo de producción del circuito impreso. Por ejemplo, una rutina podría suprimir las vías innecesarias (cada vía es una perforación, que cuesta dinero). Otras podrían redondear los bordes de las pistas, y ensanchar o mover las pistas para mantener el espacio entre éstas dentro de un margen seguro. Otra estrategia podría ser ajustar grandes áreas de cobre de tal forma que ellas formen nodos, o juntar áreas vacías en áreas de cobre. Esto permite reducir la contaminación de los productos químicos utilizados durante el grabado y acelerar la velocidad de producción.
Algunos sistemas tienen comprobación de reglas de diseño para validar la conectividad eléctrica y separación entre las distintas partes, compatibilidad electromagnética, reglas para la manufactura, ensamblaje y prueba de las tarjetas, flujo de calor y otro tipo de errores.
La serigrafía, máscara antisoldante y plantilla para la pasta de soldar, a menudo se diseñan como capas auxiliares.
Manufactura
Patrones
La gran mayoría de las tarjetas para circuitos impresos se hacen adhiriendo una capa de cobre sobre todo el sustrato, a veces en ambos lados (creando un circuito impreso virgen), y luego retirando el cobre no deseado después de aplicar una máscara temporal (por ejemplo, grabándola con percloruro férrico), dejando sólo las pistas de cobre deseado. Algunos pocos circuitos impresos son fabricados al agregar las pistas al sustrato, a través de un proceso complejo de electrorecubrimiento múltiple. Algunos circuitos impresos tienen capas con pistas en el interior de éste, y son llamados cicuitos impresos multicapas. Éstos son formados al aglomerar tarjetas delgadas que son procesadas en forma separada. Después de que la tarjeta ha sido fabricada, los componentes electrónicos se sueldan a la tarjeta.
Hay varios métodos típicos para la producción de circuitos impresos:
- La impresión serigráfica utiliza tintas resistentes al grabado para proteger la capa de cobre. Los grabados posteriores remueven el cobre no deseado. Alternativamente, la tinta puede ser conductiva, y se imprime en una tarjeta virgen no conductiva. Esta última técnica también se utiliza en la fabricación de circuitos híbridos.
- El fotograbado utiliza una Fotomecánica y grabado químico para eliminar la capa de cobre del sustrato. La fotomecánica usualmete se prepara con un fotoplotter, a partir de los datos producidos por un programa para el diseño de circuitos impresos. Algunas veces se utilizan transparencias impresas en una impresora Láser como fotoherramientas de baja resolución.
- El fresado de circuitos impresos utiliza una fresa mecánica de 2 o 3 ejes para quitar el cobre del sustrato. Una fresa para circuitos impresos funciona en forma similar a un plotter, recibiendo comandos desde un programa que controla el cabezal de la fresa los ejes x, y y z. Los datos para controlar la máquina son generados por el programa de diseño, y son almacenados en un archivo en formato HPGL o Gerber.
- La impresión en material termosensible para transferir a través de calor a la placa de cobre. En algunos sitios comentan de uso de papel glossy (fotográfico), y en otros de uso de papel con cera como los papeles en los que vienen los autoadesivos.
Tanto el recubrimiento con tinta, como el fotograbado requieren de un proceso de atacado químico, en el cual el cobre excedente es eliminado, quedando únicamente el patrón deseado.
Atacado
El atacado de la placa virgen se puede realizar de diferentes maneras. La mayoría de los procesos utilizan ácidos o corrosivos para eliminar el cobre excedente. Existen métodos de galvanoplastia que funcionan de manera rápida, pero con el inconveniente de que es necesario atacar al ácido la placa después del galvanizado, ya que no se elimina todo el cobre.
Los químicos más utilizados son el cloruro Ferrico, el sulfuro de amonio, el Ácido clorhídrico mezclado con agua y Peróxido de hidrógeno. Existen formulaciones de ataque de tipo alcalino y de tipo ácido. Según el tipo de circuito a fabricar, se considera más conveniente un tipo de formulación u otro.
Para la fabricación industrial de circuitos impresos es conveniente utilizar máquinas con transporte de rodillos y cámaras de aspersión de los líquidos de ataque, que cuentan con control de temperatura, de presión y de velocidad de transporte. También es necesario que cuenten con extracción y lavado de gases.
Perforado
Las perforaciones, o vías, del circuito impreso se taladran con pequeñas brocas hechas de carburo tungsteno.El perforado es realizado por maquinaria automatizada, controlada por una cinta de perforaciones o archivo de perforaciones. Estos archivos generados por computador son también llamados taladros controlados por computador (NCD por sus siglas en inglés) o archivos Excellon. El archivo de perforaciones describe la posición y tamaño de cada perforación taladrada.
Cuando se requieren vías muy pequeñas, taladrar con brocas es costoso, debido a la alta tasa de uso y fragilidad de éstas. En estos casos, las vías pueden se evaporadas por un Láser. Las vías perforadas de esta forma usualmente tienen una terminación de menor calidad al interior del orificio. Estas perforaciones se llaman micro vías.
También es posible, a través de taladrado con control de profundidad, perforado láser, o pre-taladrando las láminas individuales antes de la laminación, producir perforaciones que conectan sólo algunas de las capas de cobre, en vez de atravesar la tarjeta completa. Estas perforaciones se llaman vías ciegas cuando conectan una capa interna con una de las capas exteriores, o vías enterradas cuando conectan dos capas internas.
Las paredes de los orificios, para tarjetas con dos o más capas, son metalizadas con cobre para formar, orificios metalizados, que conectan eléctricamente las capas conductoras del circuito impreso.
Estañado y máscara antisoldante
Los pads y superficies en las cuales se montarán los componentes, usualmente se metalizan, ya que el cobre al desnudo no es soldable fácilmente. Tradicionalmente, todo el cobre expuesto era metalizado con Soldadura. Esta soldadura solía ser una aleación de plomo-estaño, sin embargo, se están utilizando nuevos compuestos para cumplir con la directiva RoHS de la UE, la cual restringe el uso de plomo. Los conectores de borde, que se hacen en los lados de las tarjetas, a menudo se metalizan con oro. El metalizado con oro a veces se hace en la tarjeta completa.
Las áreas que no deben ser soldadas pueden ser recubiertas con un polímero resistente a la soldadura, el cual evita cortocircuitos entre las patas cercanas de un componente.
Serigrafía
Los dibujos y texto se pueden imprimir en las superficies exteriores de un circuito impreso a través de la serigrafía. Cuando el espacio lo permite, el texto de la serigrafía puede indicar los nombres de los componentes, la configuración de los interruptores, puntos de prueba, y otras características útiles en el ensamblaje, prueba y servicio de la tarjeta. También puede imprimirse a través de tecnología de impresión digital por chorro de tinta (inkjet/Printar) y volcar información variable sobre el circuito (serialización, codigos de barra, información de trazabilidad).
Montaje
En las tarjetas through hole (a través del orificio), las patas de los componentes se insertan en los orificios, y son fijadas eléctrica y mecánicamente a la tarjeta con soldadura.
Con la tecnología de montaje superficial, los componentes se sueldan a los pads en las capas exteriores de la tarjetas. A menudo esta tecnología se combina con componentes through hole, debido a que algunos componentes están disponibles sólo en un formato.
Pruebas y verificación
Las tarjetas sin componentes pueden ser sometidas a pruebas al desnudo, donde se verifica cada conexión definida en el netlist en la tarjeta finalizada. Para facilitar las pruebas en producciones de volúmenes grandes, se usa una Cama de clavos para hacer contacto con las áreas de cobre u orificios en uno o ambos lados de la tarjeta. Un computador le indica a la unidad de pruebas eléctricas, que envíe una pequeña corriente eléctrica a través de cada contacto de la cama de clavos, y que verifique que esta corriente se reciba en el otro extremo del contacto. Para volúmenes medianos o pequeños, se utilizan unidades de prueba con un cabezal volante que hace contacto con las pistas de cobre y los orificios para verificar la conectividad de la placa verificada.
Protección y paquete
Los circuitos impresos que se utilizan en ambientes extremos, usualmente tienen un recubrimiento, el cual se aplica sumergiendo la tarjeta o a través de un aerosol, después de que los componentes han sido soldados. El recubrimiento previene la corrosión y las corrientes de fuga o cortocircuitos producto de la condensación. Los primeros recubrimientos utilizados eran ceras. Los recubrimientos modernos están constituidos por soluciones de goma silicosa, poliuretano, acrílico o resina epóxica. Algunos son plásticos aplicados en una cámara al vacío.
Tecnología de montaje superficial
La tecnología de montaje superficial fue desarrollada en la década de 1960, ganó impulso en Japón en la década de 1980, y se hizo popular en todo el mundo a mediados de la década de 1990.
Los componentes fueron mecánicamente rediseñados para tener pequeñas pestañas metálicas que podían ser soldadas directamente a la superficie de los circuitos impresos. Los componentes se hicieron mucho más pequeños, y el uso de componentes en ambos lados de las tarjetas se hizo mucho más común, permitiendo una densidad de componentes mucho mayor.
El montaje superficial o de superficie se presta para un alto grado de automatización, reduciendo el costo en mano de obra y aumentando las tasas de producción. Estos dispositivos pueden reducir su tamaño entre una cuarta a una décima parte, y su costo entre la mitad y la cuarta parte, comparado con componentes through hole.